adjar.id – Adjarian, di bawah ini adalah pembahasan soal matematika materi menghitung luas segitiga.
Soal-soal tersebut dimuat di buku paket Senang Belajar Matematika pada halaman 143 sampai 144.
Masih ingat bangun datar segitiga, kan?
Yap! Segitiga merupakan bangun datar yang mempunyai tiga sisi yang membentuk tiga sudut.
Terdapat macam-macam jenis segitiga, di antaranya adalah segitiga sama sisi, siku-siku, sama kaki, hingga segitiga sembarang.
Nah, pada segitiga jenis sama sisi, sama kaki, dan sembarang, dapat ditarik garis tengah yang nantinya membentuk sisi tinggi.
Sisi tinggi inilah yang merupakan salah satu komponen untuk menghitung luas segitiga.
Secara umum, rumus luas segitiga adalah “1/2 x a x t”, di mana “a” adalah sisi alas dan “t” adalah sisi tinggi.
Sekarang kita simak pembahasan soalnya, yuk!
Baca Juga: 6 Jenis Segitiga
Ayo Mencoba
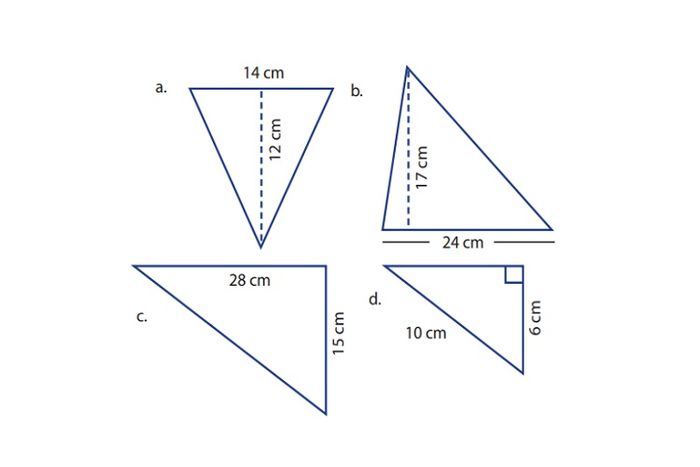
1. Tentukan luas segitiga berikut!
Menghitung luas segitiga, soal nomor 1.
Pembahasan: Pada soal, terdapat tiga jenis segitiga yang berbeda, yaitu segitiga sama kaki, segitiga sembarang, dan segitiga siku-siku.
Meski berbeda, kita akan tetap menghitungnya menggunakan rumus luas segitiga yang sama, Adjarian.
a. Diketahui alas segitiga 14 cm dan tingginya 12 cm
Luas (L) = 1/2 x a x t
L = 1/2 x 14 x 12
L = 84 cm2
Jadi, luas segitiga a adalah 84 cm2.
Baca Juga: Ciri-Ciri Segitiga Siku-Siku, Segitiga Sama Kaki, dan Segitiga Sama Sisi
b. Diketahui alas segitiga 24 cm dan tingginya 17 cm
Luas (L) = 1/2 x a x t
L = 1/2 x 24 x 17
L = 204 cm2
Jadi, luas segitiga b adalah 204 cm2.
c. Diketahui alas segitiga 15 cm dan tingginya 28 cm
Luas (L) = 1/2 x a x t
L = 1/2 x 15 x 28
L = 210 cm2
Baca Juga: Mengenal Sudut Dalam dan Sudut Luar Segitiga
Jadi, luas segitiga c adalah 210 cm2.
d. Diketahui alas segitiga 6 cm dan sisi miringnya 10 cm
Nah, karena tingginya belum diketahui, maka kita akan menghitungnya menggunakan rumus pitagoras.
Tinggi = Siri miring – alas
Tinggi = 102 – 62
Tinggi = 642
Tinggi = √64
Tinggi = 8
Luas (L) = 1/2 x a x t
Baca Juga: Rumus Keliling Segitiga Siku-Siku dan Contoh Soalnya
L = 1/2 x 6 x 8
L = 24 cm2
Jadi, luas segitiga d adalah 24 cm2
2. Tentukan alas atau tinggi segitiga berikut!
Mencari sisi alas dan tinggi segitiga, soal nomor 2.
Pembahasan: Perkebalikan dengan soal sebelumnya, kali ini kita diminta untuk mencari sisi alas atau tinggi dengan luas yang sudah diketahui.
Untuk mencarinya, kita tetap bisa menggunakan rumus luas, Adjarian.
a. Diketahui tinggi 13 cm dan luas 52 cm2
L = 1/2 x a x t
52 cm2 = 1/2 x a x 13
Baca Juga: Menghitung Rumus Luas Segitiga Sama Sisi dan Sifatnya
a = 52 x 2 : 13
a = 8 cm
Jadi, panjang alas segitiga a adalah 8 cm.
b. Diketahui alas 25 cm dan luas 125 cm2
L = 1/2 x a x t
t = 2 x L : a
t = 2 x 125 : 25
t = 250 : 25
t = 10 cm
Baca Juga: Rumus Luas Segitiga Sembarang dan Sifat-Sifatnya
Jadi, tinggi segitiga b adalah 10 cm
c. Diketahui tinggi 18 cm dan luas 234 cm2
L = 1/2 x a x t
a = 2 x L : t
a = 2 x 234 : 18
a = 468 : 18
a = 26 cm
Jadi, panjang alas segitiga c adalah 26 cm.
Nah, itulah pembahasan soal matematika materi menghitung luas segitiga, Adjarian.
Baca Juga: Bangun Datar Segitiga: Jenis, Ciri-Ciri, dan Rumusnya
Tonton video ini, yuk!
| Penulis | : | Jestica Anna |
| Editor | : | Rahwiku Mahanani |
KOMENTAR